Biểu đồ Histogram là một sáng kiến được phát hiện bởi nhà toán học người Anh – Karl Pearson. Với tính năng thể hiện sự phân bố dữ liệu một cách trực quan, biểu đồ tần suất mang nhiều lợi ích trong quy trình thống kê và báo cáo số liệu. Để hiểu và sử dụng thành thạo biểu đồ này, bạn có thể tìm hiểu những thông tin mà chúng tôi chia sẻ dưới đây.

Biểu đồ Histogram là gì?
Biểu đồ histogram còn gọi là biểu đồ tần suất, là đồ thị thống kê biểu diễn sự phân bố của một tập dữ liệu liên tục thông qua các cột được vẽ, mỗi cột biểu diễn một loại hoặc khoảng lớp cụ thể. Chiều cao của thanh phản ánh tần suất hoặc số lượng điểm dữ liệu trong mỗi nhóm.
Về bản chất, biểu đồ histogram tiết lộ các mẫu, xu hướng và thông tin chi tiết ẩn trong dữ liệu thô, không có thứ tự – thể hiện một bức tranh có tổ chức giúp việc diễn giải và phân tích dễ quản lý và hiệu quả hơn.

Tiện ích của biểu đồ tần suất được ứng dụng trên nhiều ngành công nghiệp và lĩnh vực khác nhau bao gồm tài chính, y tế công cộng, khoa học môi trường, sản xuất và nghiên cứu xã hội. Nó rất quan trọng đối với các nhiệm vụ như xác định các mẫu trong các tập dữ liệu lớn, phát hiện các giá trị ngoại lệ, đảm bảo kiểm soát chất lượng, ước tính các tham số thống kê và truyền đạt hiệu quả các phát hiện cho các bên liên quan. Đây được xem là một trong 7 công cụ quản lý chất lượng được sử dụng phổ biến.
Các loại biểu đồ Histogram
Biểu đồ histogram đồng đều
Phân phối đồng đều cho thấy số lượng lớp quá nhỏ và mỗi lớp có cùng số phần tử, có thể bao gồm một số đỉnh.

Biểu đồ histogram hai đỉnh
Nếu biểu đồ phân bố có hai đỉnh, thì nó được gọi là Bimodal. Nó xảy ra khi tập dữ liệu có các quan sát trên hai loại cá nhân khác nhau hoặc các nhóm kết hợp nếu các tâm của hai histogram riêng biệt đủ xa so với sự thay đổi trong cả hai tập dữ liệu.

Biểu đồ histogram đối xứng
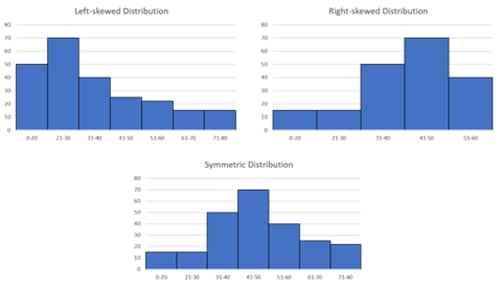
Histogram đối xứng còn được gọi là histogram hình chuông. Khi bạn vẽ đường thẳng đứng xuống giữa histogram và hai bên có kích thước và hình dạng giống hệt nhau, histogram được gọi là đối xứng. Biểu đồ được coi là đối xứng hoàn hảo nếu nửa bên phải của hình ảnh giống với nửa bên trái. Còn nếu Histogram không đối xứng được gọi là lệch.

Ngoài ra, còn một số dạng phân phối biểu đồ tần suất khác như:
Phân phối lệch: Là khi đỉnh của mô hình phân phối lệch về 1 bên trái hoặc phải.
Phân phối cao nguyên: Loại phân phối xuất hiện nhiều đỉnh dữ liệu nằm liền kề nhau, nó được hình thành khi có nhiều quá trình thu thập dữ liệu khác nhau.

Phân phối đỉnh cạnh: Loại này có một đỉnh dữ liệu lớn ở một bên, nguyên nhân dẫn đến điều này có thể do xuất hiện lỗi trong việc tạo biểu đồ Histogram.

Phân phối lược: Có thể hình dung các thanh biểu đồ Histogram trong phân phối này được xen kẽ cao và thấp.

Phân phối bị cắt: Là loại phân phối trong đó các đuôi của biểu đồ bị cắt ngang do nhà cung cấp chỉ cung cấp dữ liệu ở một phạm vi nhất định.

Phân phối Food Dog: Dữ liệu chỉ tập trung phân bổ ở hai bên của biểu đồ và chưa một khoảng trống ở giữa. Đa phần xảy ra tình trạng này là do doanh nghiệp cung cấp hai loại sản phẩm khác nhau.

Sự khác biệt giữa biểu đồ tần suất và biểu đồ thanh
Biểu đồ Histogram nhìn sơ qua trông rất giống với biểu đồ thanh, nhưng thực tế giữa hai biểu đồ này có những điểm đặc trưng khác nhau, hãy xem qua bảng so sánh dưới đây:
| Biểu đồ Histogram | Biểu đồ thanh |
| Hình hai chiều | Hình một chiều |
| Tần số được thể hiện bằng diện tích của mỗi hình chữ nhật | Chiều cao thể hiện tần suất, còn chiều rộng không có ý nghĩa. |
| Cho thấy các hình chữ nhật chạm vào nhau | Các hình chữ nhật tách biệt nhau bằng các khoảng cách bằng nhau. |
Để giúp các bạn hình dung rõ hơn, hãy xem 2 hình dưới đây:


Khi nào nên và không nên sử dụng Histogram?
Nên sử dụng biểu đồ histogram trong trường hợp:
- Khi dữ liệu có một biến độc lập duy nhất như độ tuổi của khách hàng. Biểu đồ histogram giúp người xem hiểu được sự phân phối của biến phụ thuộc. Ví dụ, số tiền ngân hàng của khách hàng dựa trên độ tuổi của họ.
- Khi dữ liệu có phạm vi liên tục như điểm kiểm tra của học sinh. Khi dữ liệu có khoảng cách đáng kể trong phạm vi của nó, biểu đồ histogram có thể không phù hợp.
- Khi hai tập dữ liệu cần được so sánh, ví dụ hãy xem xét số lượng mua hàng của khách hàng ở các nhóm tuổi khác nhau. Biểu đồ histogram có thể được sử dụng để so sánh dữ liệu này trên nhiều cửa hàng.
Không nên sử dụng biểu đồ histogram trong trường hợp:
- Khi dữ liệu không phải là số: Biểu đồ histogram phù hợp nhất để biểu diễn đồ họa của một biến số có phạm vi dữ liệu liên tục. Nếu dữ liệu bao gồm các giá trị không phải số như giới tính hoặc vị trí, thì biểu đồ histogram sẽ không phù hợp.
- Khi kích thước mẫu nhỏ: Biểu đồ tần suất hoạt động tốt khi có đủ điểm dữ liệu trong mẫu. Khi có quá ít điểm dữ liệu, biểu đồ không thể trực quan hóa phân phối dữ liệu. Theo nguyên tắc chung, biểu đồ histogram hữu ích khi có 20 mẫu trở lên.
- Khi có khoảng cách lớn trong dữ liệu: Biểu đồ histogram phù hợp nhất khi dữ liệu mẫu là liên tục, nên biểu đồ sẽ không hiệu quả khi thiếu dữ liệu hoặc không xác định.
Ứng dụng của biểu đồ Histogram
Phân tích phân phối tần suất
Biểu đồ tần suất rất hữu ích để phân tích phân phối tần suất của dữ liệu mẫu. Trong một thí nghiệm thống kê, phân phối tần suất là số lượng quan sát thuộc về một danh mục cụ thể.
Xem ví dụ bên dưới, biểu đồ thể hiện số lượng hành vi mua sắm của khách hàng thuộc các nhóm tuổi khác nhau. Qua quan sát, có thể thấy cụ thể rằng khách hàng thuộc nhóm tuổi từ 50 – 70 đã thực hiện lượng mua sắm cao nhất.

Phân tích đối xứng dữ liệu
Với biểu đồ tần suất, người xem có thể phân tích bản chất của phân phối tần suất, cụ thể như:
- Một số phân phối có thể đối xứng, nghĩa là giá trị trung bình của phân phối chính xác quanh giá trị giữa của tập dữ liệu.
- Một số phân phối có thể không đối xứng mà lệch trái hoặc lệch phải. Điều này cho thấy giá trị trung bình của dữ liệu nằm ở đầu hoặc cuối phạm vi dữ liệu.
- Một số dữ liệu sẽ có phân phối đồng đều trong đó mọi danh mục có số điểm dữ liệu gần như bằng nhau.
Phân tích sự thay đổi theo thời gian
Biểu đồ tần suất có thể phân tích kết quả quy trình thay đổi theo thời gian. Ví dụ, doanh nghiệp có thể theo dõi số lượng sản phẩm lỗi được sản xuất trong một ca làm việc tại nhà máy. Nhờ đó, doanh nghiệp có thể sử dụng dữ liệu này để xác định những giờ có nhiều lỗi xảy ra nhất và đưa ra các biện pháp phòng ngừa kịp thời.
Hướng dẫn cách vẽ biểu đồ Histogram
Sử dụng công cụ Excel
Để tạo biểu đồ tần suất trong Excel bạn cần cài đặt phiên bản Excel từ 2016 trở lên.
Lấy ví dụ: Một tệp dữ liệu có 41 scores (điểm số) và chúng ta muốn xây dựng một biểu đồ Histogram để phân chia các điểm số này thành các khoảng cách nhau 10 điểm (nhỏ nhất là 40 và lớn nhất là 100). Các bước thực hiện:
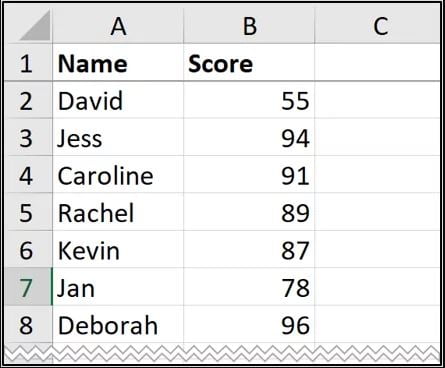
Bước 1. Chọn ô A1:B42.
Bước 2: Nhấp vào Insert
Bước 3: Insert Statistic Chart
Bước 4: Histogram.
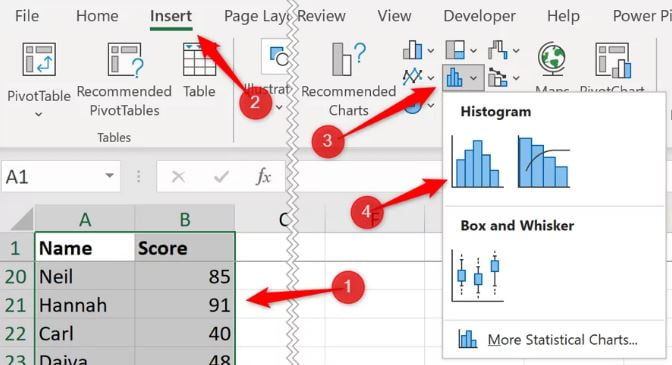
Sau đó, biểu đồ Histogram đã được hình thành và tạo thành 4 cột (bin) liền nhau như bên dưới.
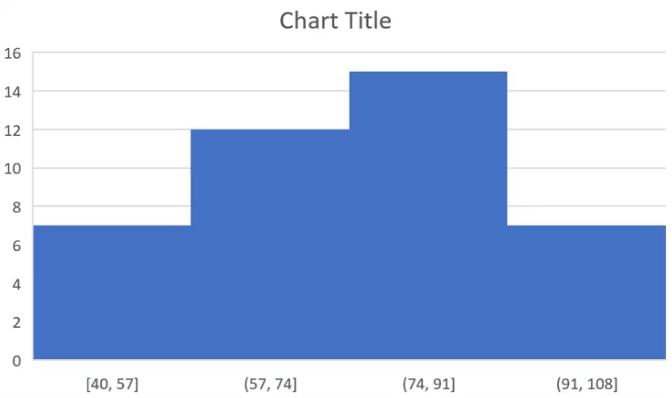
Bước 5:
- Nhấp chuột phải vào trục danh mục (trục x) và nhấp vào Format Axis .
- Nhấp vào danh mục Axis Options .
- Nhập 40 cho Underflow bin. Đây là số điểm mà bins sẽ bắt đầu từ đó.
- Nhập 90 cho Overflow bin. Điểm từ 91 trở lên sẽ được tính vào bin cuối cùng này.
- Chỉ định Bin width là 10 . Điều này tạo ra bins trong khoảng thời gian từ 10 đến 40.
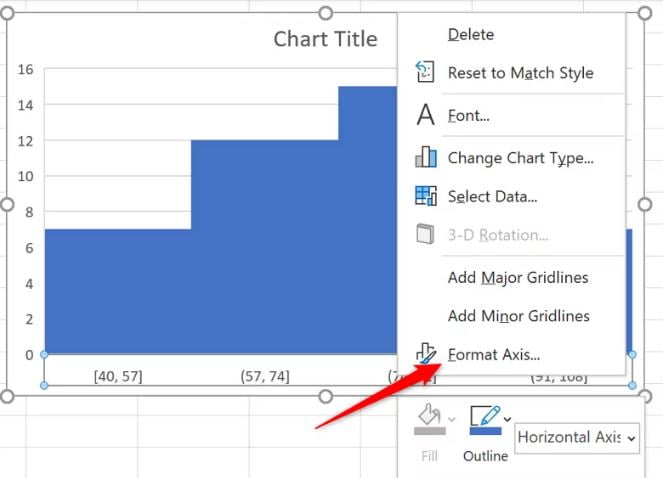
Một cách khác để chỉ định chiều rộng cột là sử dụng option để chỉ định số lượng cột được yêu cầu.
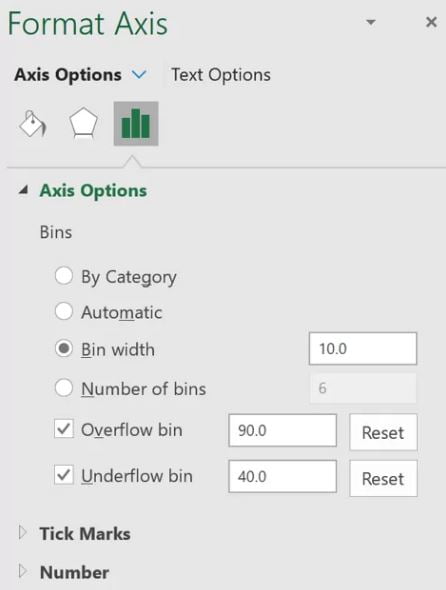
Kết quả:
Bạn có thể thực hiện các chỉnh sửa cho biểu đồ như, tiêu đề, danh mục và màu sắc của các cột.

Ưu điểm của việc cách tạo này là không cần chuẩn bị trước các cột hoặc ghi nhớ các công thức phức tạp. Tất cả đều được tích hợp qua chức năng built-in chart và các tùy chọn có sẵn.
Nhược điểm là cách làm này chỉ có trong Excel 2016 trở lên và có một số tính năng bị giới hạn và thiếu sự linh hoạt.
Sử dụng công thức
Sử dụng công thức là phương pháp mang lại sự linh hoạt hơn, nó có thể sử dụng ở tất cả các phiên bản của Excel. Phương pháp này bao gồm việc chèn biểu đồ cột thay vì tùy chọn Histogram.
Chúng tôi sẽ dùng lại dữ liệu đã sử dụng trong ví dụ trước, nhưng hai điểm thi được thay đổi thành dưới 40.
Đầu tiên, hãy nhập dữ liệu cho biểu đồ. Đây là các thanh và tần suất điểm thi trong mỗi thanh đó.
Các thanh được gõ vào phạm vi G4:G10 và hàm COUNTIFS được sử dụng để đếm số lần xuất hiện của điểm thi cho mỗi thanh.
Hàm: =COUNTIFS($B$2:$B$42,”>=”&E4,$B$2:$B$42,”<=”&F4)
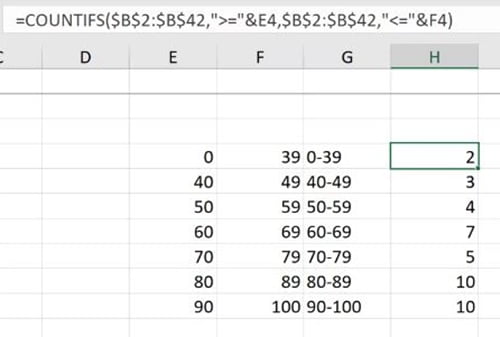
Các giá trị trong khoảng E4:E10 và F4:F10 được sử dụng để hỗ trợ hàm COUNTIFS.
Để tạo biểu đồ Histogram:
Bước 1: Chọn phạm vi G4:H10
Bước 2: Nhấp vào Insert
Bước 3: Insert Column or Bar Chart
Bước 4: Clustered Column.
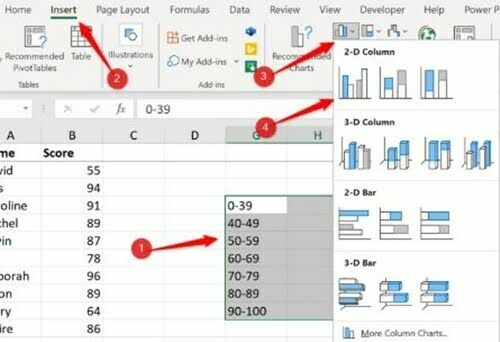
Kết quả:
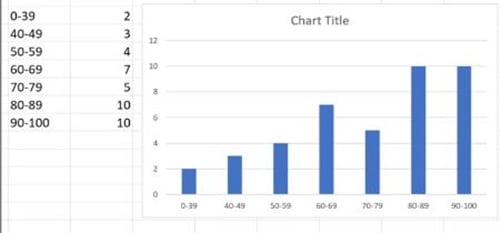
Bước 5: Thực hiện các thay đổi:
- Chỉnh sửa tiêu đề biểu đồ thành “Exam Score Distribution”
- Định dạng các cột thành màu xanh lá cây
- Xóa trục giá trị (trục y)
- Xóa các đường lưới ngang
- Thêm nhãn dữ liệu phía trên mỗi cột
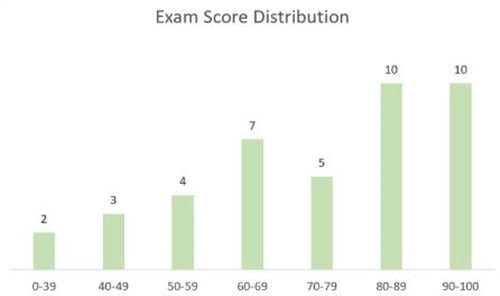
Bước 6: Để xóa khoảng cách giữa các cột, nhấp chuột phải vào một trong các cột và nhấp vào Format Data Series.
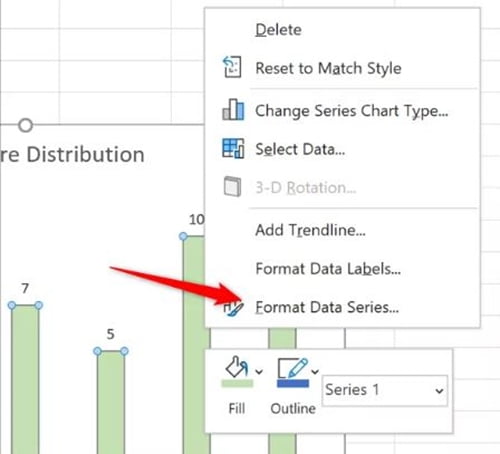
Bước 7: Từ ngăn Format Data Series, nhấp vào danh mục Series Options và thay đổi Gap Width thành 0.
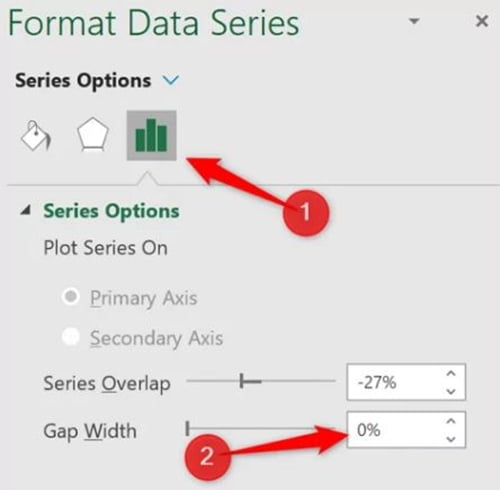
Khoảng cách giữa các cột bị xóa là hiển thị biểu đồ Histogram như bên dưới.
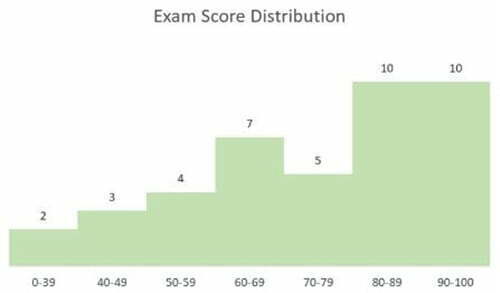
Bằng cách tạo các cột riêng, phương pháp mang đến nhiều sự linh hoạt hơn. Cột đầu tiên dành cho điểm thi dưới 40, các cột sau cách nhau 10 điểm. Biểu đồ này dễ dàng được cập nhật khi chỉnh sửa các giá trị trong các ô của dữ liệu nguồn.
Tóm lại, trong số các công cụ trực quan hóa dữ liệu khác nhau, thì biểu đồ histogram nổi bật vì tính đơn giản, tính linh hoạt và giá trị thông tin sâu sắc. Histogram không chỉ cung cấp trực quan về phân phối dữ liệu mà còn đặt nền tảng cho các phân tích thống kê nâng cao hơn. Để thực hiện được điều đó, chúng tôi giới thiệu quý độc giả khóa học 07 công cụ quản lý chất lượng, sẽ giúp bạn biết cách vận dụng các biểu đồ thống kế sản xuất hiệu quả nhất hiện nay như:








Đăng ký nhận bản tin
Hãy gửi thông tin để không bỏ sót bất kỳ tin tức hoặc chương trình khuyến mãi từ Học Viện PMS